A Gömböc egy konvex, homogén anyagú test, amelynek 1 stabil és 1 instabil egyensúlyi helyzete van vízszintes felületen. Inhomogén anyagból könnyű Gömböc-szerű testet készíteni, ilyen például a keljfeljancsi. A konvexitás is fontos kikötés: a konkáv testek nem mindig a felületükön gördülnek, emiatt konkáv Gömböcöt is könnyű létrehozni.
Az egyetlen stabil helyzettel rendelkező formákat monostatikusnak nevezzük, az egyetlen stabil és egyetlen instabil egyensúllyal rendelkező formákat pedig mono-monostatikusnak. A Gömböc tudományos néven tehát az első konvex, homogén mono-monostatikus test.
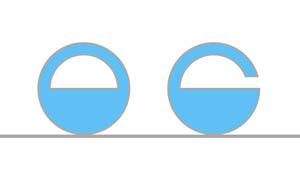
Kétdimenziós Gömböc
Minden 2 dimenziós konvex alakzat leírható súlypontja (G) körüli poláris koordinátarendszerben egy R(α) függvénnyel.
Vízszintes felületre helyezve minden test úgy kezd gördülni, hogy a súlypontja alacsonyabbra kerüljön, tehát úgy, hogy a felülettel érintkező pontban R csökkenjen.
A test akkor van egyensúlyban, ha a felülettel érintkező pontjában dR/dα = 0. Az egyensúly stabil R minimumainál (d2R/dα2 > 0) és instabil a maximumhelyeken (d2R/dα2 < 0).
Mivel az R függvénynek felváltva követik egymást a lokális minimum és maximumhelyei, ezért a stabil és instabil egyensúlyi helyzetek száma egyenlő.
Ezen kívül
minden síkbeli konvex, homogén testnek legalább 2 stabil és 2 instabil egyensúlya van.
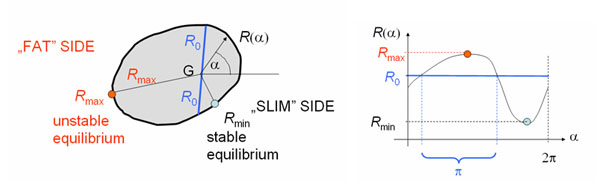
Ha lenne olyan test, amelynek csak 1+1 egyensúlya van, az ahhoz tartozó R(α) függvény diagramja egyetlen minimumot, illetve maximumot tartalmazna. Ekkor egy R = R0 vízszintes egyenessel a diagram kettévágható lenne úgy, hogy a függvény R > R0 és R < R0 részének is π hosszúságú a vízszintes vetülete. Ez megfelelne az eredeti test súlyponton átmenő egyenessel való kettévágásának egy sovány (R < R0) és egy kövér (R > R0) részre. Ez viszont azt jelentené, hogy a súlypontnak a „kövér” oldalon kellene lennie, nem pedig középen. Mivel a súlypontnak középen kell lennie, ellentmondásra jutottunk – tehát a tétel igaz.
Síkban tehát nem létezhet a Gömböcnek megfelelő test.
Ez a meglepően egyszerű állítás egy régóta ismert matematikai tétel fizikai megfelelője:
Egy egyszerű, zárt síkgörbe görbületének legalább négy lokális szélsőértéke van.
A Négycsúcs-tételnek számtalan általánosítása és közeli rokona van a geometriában, amelyeket néha együttesen hívnak Négycsúcs-tételeknek. Ha térben nem létezne Gömböc, az is a ‘Négycsúcs-tételek’ közé tartozó eredmény lehetne.
A Gömböc alapötlete

R lokális minimumai és maximumai itt is stabil, illetve instabil egyensúlyoknak felelnek meg, de a test egyensúlyban van R nyeregpontjaiban is.
A Poincaré-Hopf tétel szerint a háromféle egyensúly száma gömbbel izomorf testek esetén ki kell, hogy elégítse az s+i-n=2 egyenlőtlenséget. Az 1. tételnek térben több megfelelője képzelhető el:
- a) s > 1,
- b) i > 1,
- c) s + i > 2,
ezek közül a) és b) könnyen cáfolható:
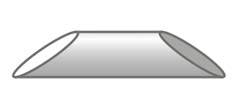
i > 1-re is egyszerűen lehet ellenpéldát találni:
ennél a testnél i = n = 1, s = 2:
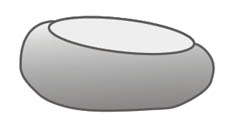
A harmadik lehetőség maga a Gömböc kérdése: létezik-e olyan térbeli konvex, homogén test, melyre s = i = 1 (és emiatt n = 0)?
Megpróbálhatjuk alkalmazni a síkbeli bizonyítást annak igazolására, hogy nincs ilyen.
Ha lenne ilyen, akkor R(ϕ,ϴ) -nak egyetlen lokális maximuma és minimuma lenne. A test felülete ez esetben is kettéosztható lenne egy R = R0 szintvonallal egy kövér és egy sovány részre, amelyek azonos nagyságúak (azaz G-ből nézve azonos nagyságú térszögben látszanak).
Ha ez a szintvonal egy síkgörbe (azaz kör), akkor a síkbeli esethez hasonlóan ellentmondásra jutunk. Lehet azonban térgörbe is, mint például a teniszlabdák felületéről ismert vonal. Ez esetben hiába osztja fel a vonal a testet pl. egy felső „kövér” és egy alsó „sovány” részre, ebből nem következik, hogy a súlypontnak a felső oldalon kell lennie. A síkbeli bizonyítás tehát térben nem alkalmazható.
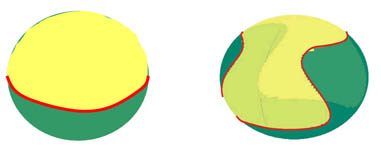
A bizonyítás „sikertelensége” ad támpontot arra nézve, hogy ha létezik térbeli Gömböc, akkor az hogyan nézhet ki. Ebből kiindulva sikerült egy olyan két paraméteres zárt képletet létrehozni, amelyről analitikusan bizonyítható, hogy létezik olyan paraméter-pár, ahol az eredményül kapott testre s = i = 1.
Sajnos a kapott test konvex is kell legyen, és ez a képletünknél csak úgy lehetséges, ha a forma észrevehetetlen mértékben tér el a gömbtől. Ezzel a Gömböc létezése elméletben bebizonyosodott, de kézzelfogható forma léte továbbra is kérdéses maradt.

A kézzelfogható Gömböc
Az elméleti Gömböc megalkotása után felvetődött a kérdés: vajon miért csak elvben sikerült Gömböcöt előállítanunk?
Vagy a konstruált képlet nem volt elég jó, vagy valami mélyebb oka van a sikertelenségnek. A tény, hogy a Gömböc-szerű formák bizonyíthatóan gömbszerűek, valamint az ilyen típusú formák hiánya a rhodoszi kavicsokban azt sugallta, hogy valami miatt nincsenek markáns, a gömbtől jelentősen eltérő formák, melyekre s = i = 1.
Mégis az derült ki, hogy más oldalról megközelítve előállítható egy gyakorlatban létező Gömböc is. Az alábbi konstrukció a fenti teniszlabdás ötleten alapszik; egyszerű másodrendű felületekből (henger, ellipszoid, kúp) és síklapokból épül fel.
Az új test nyilvánvalóan konvex; numerikus integrálással kimutatható, hogy a súlypontja kicsivel az ábra origója alatt van, és ebből egyszerűen belátható, hogy valóban mono-monostatikus. Természetesen végtelen sok hasonló tulajdonságú forma létezik, az ábra ezek közül egy változatot mutat.
Az eddig elkészült Gömböcök abban térnek el ettől a verziótól, hogy több felületből állnak, ezzel stabil egyensúlyuk stabilabb és működésük is látványosabb.


Irodalom
Journal of Elasticity
Static equilibria of planar, rigid bodies: Is there anything new?
G. Domokos, J. Papadopulos, A. Ruina • 36 pp. 59-66, 1994.
Journal of Nonlinear Science
Static Equilibria of Rigid Bodies: Dice, Pebbles, and the Poincaré-Hopf Theorem
P. L. Várkonyi, G. Domokos • Vol 16: pp 255-281, 2006.
– A testek elméleti osztályozása az egyensúlyok száma alapján
– Valódi kavicsok osztályozása Rodoszon – nincs köztük Gömböc
– A Kolumbusz algoritmus
– A 2D-s Gömböc nemléte és a négy csúcs tétel közötti kapcsolat.
The Mathematical Intelligencer
My Lunch with Arnold
G. Domokos • 28 (4) pp. 31-33, 2006.
– Arnold és a Gömböc sejtése
The Mathematical Intelligencer
Mono-monostatic Bodies: The Answer to Arnold's Question
P. L. Várkonyi, G. Domokos • 28 (4) pp34-38 (2006)
– a Gömböc gömbszerűsége
– a Gömböc és a teknősök kapcsolata
