The Gömböc and the sphere
There is a close relationship between the Gömböc and the sphere. There are quantitative definitions of the flatness and the thinness of a given shape. According to a straightforward version of this definition, the minima of both quantities are 1. For the sphere, both are 1 as they are for Gömböc-type bodies, but for no other ones. Thus, the Gömböc is the most sphere-like body (apart from spheres). This fact inspired its Hungarian name ( ‘Gömböc’ is the name of a sort of traditional Hungarian butchers’ product of sphere-like shape; it also appears in folk tales).

Sensitivity

The Gömböc in Nature

Natural abraison decreases the number of balance points, approaching the Gömböc as an unattainable end point. This theory
- proved ancient fluvial activities on Mars and
- provided a philosophic frame to shape evolution where the starting point appears to be the (statistical average of the) cube confirming Plato’s postulate who identified the element Earth with the cube.
The Gömböc as "stem-stone"
A Gömböc mint "őstest"
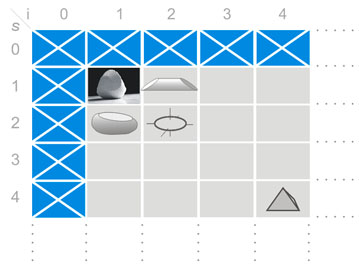
One can classify shapes by number and type of their equilibria when placed on a horizontal surface. In this respect, all classes can be generated from the Gömböc, but the reverse is not true: the existence of the Gömböc cannot be deduced from the existence of other shapes. This property shows analogy to the ‘stem-cells’ in biology: stem-cells can transform into arbitrary specialized cells, however they cannot be created from the specialized ones.
The classification of bodies based on the number of their stable (s) and unstable (u) points can be visualized in a table, in which rows and columns correspond to different values of s and u, respectively. (The number of saddle-type balance points can be determined as s + u – 2). The majority of pebbles belongs to cell (2,2). The regular tetrahedron is of class (4,4): it lies stably on its 4 facets, unstably on its 4 vertices; standing on either of its 6 edges are saddle-type equilibria (i.e. it can lurch in these positions but only in some directions). The Gömböc is in the upper-left (1,1) corner of the table.
The number of equilibria can be increased by small changes of a shape. If, for example, a small piece around the vertex of a cube is adequately chopped off, it can stay stably on this vertex. Also, “the egg of Columbus” works this way.